Unwrapped Interferograms: Creating a Deformation Map

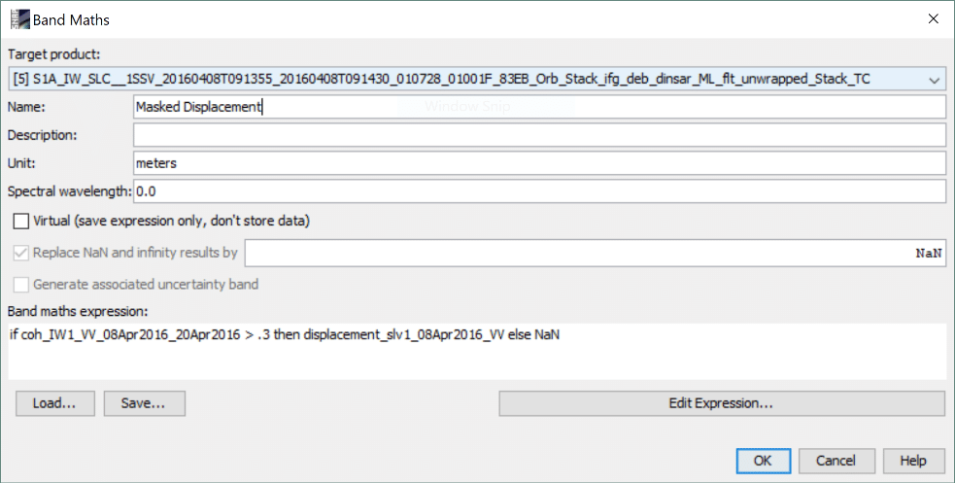
Continuing from the recipe How to Phase Unwrap an Interferogram, this final InSAR recipe will bring our unwrapped phase information out of abstraction into actual displacement units (meters). This recipe will go over the steps of converting the phase values to line-of-sight or vertical displacements as well as discarding data of low correlation that is likely unreliable.

Interpretation

Coherence

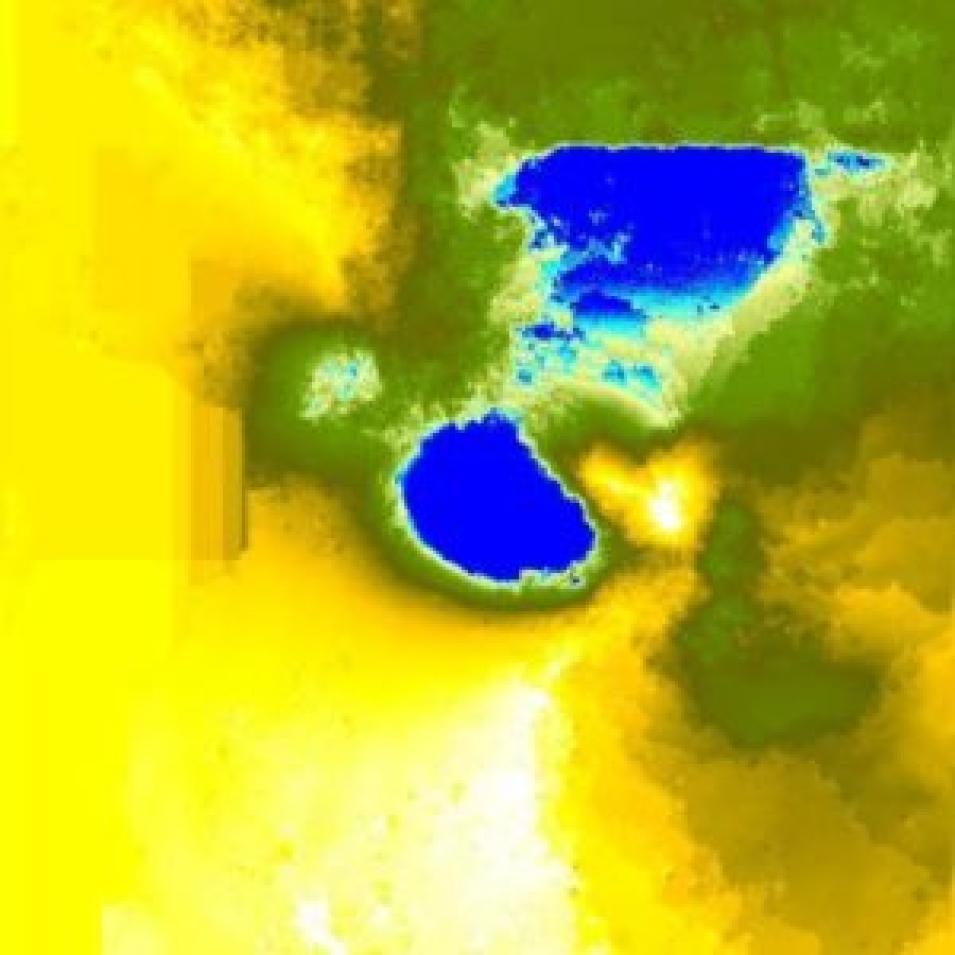
Coherence values must also be recognized in order to assess the validity of our displacement map. In general, coherence is the relative uniformity of phase difference between two interfering waves. In the context of SAR interferometry, this assessment is estimated from the random noise and amplitude differences that exist within a resolution cell, or pixel as viewed in the S1TBX. Areas of decorrelation (loss of coherence) should be ignored when interpreting accurate displacement values.

Coherence loss is cumulative from multiple sources:

Temporal changes such as the growth of vegetation or snow fall
A low signal-to-noise ratio
Weak signal return
Altitude changes in the range or azimuth directions (coherence is most severe when this difference is within a resolution cell)

This recipe will go over the steps necessary to remove incoherent data from the displacement map.

Geometry

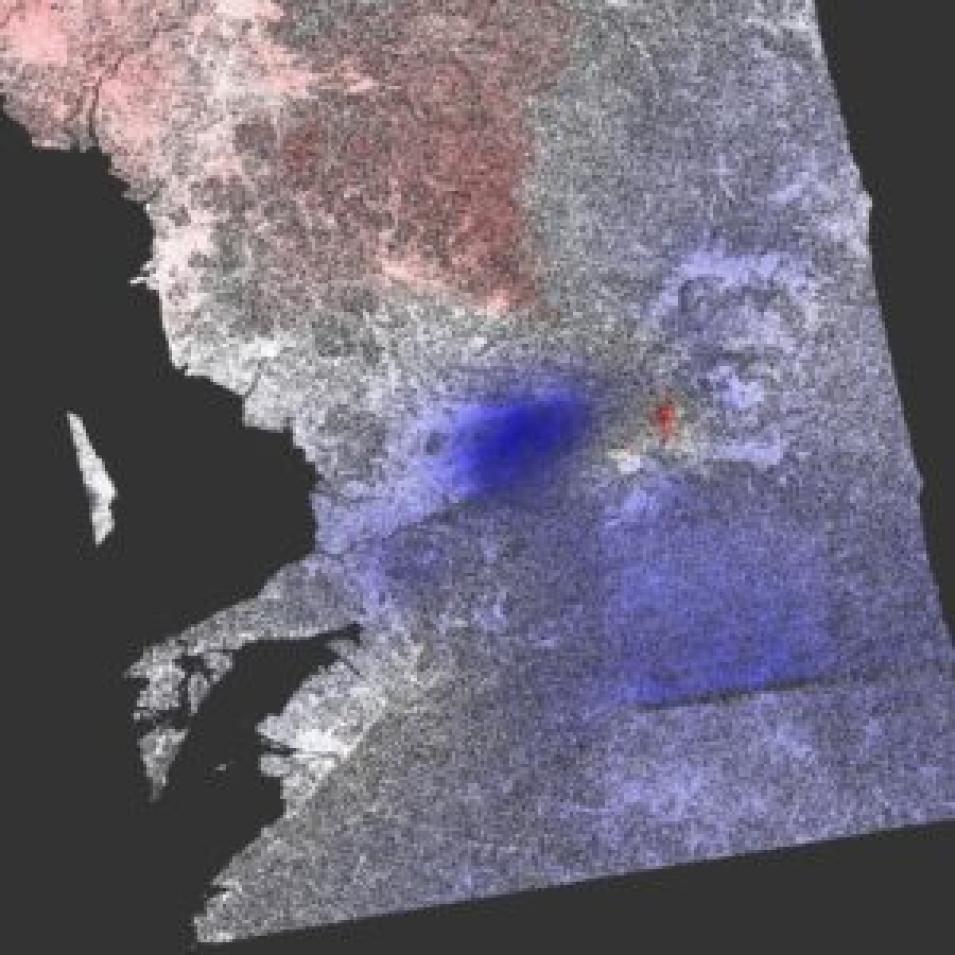
The displacement values themselves can also be ambiguous. First, they are a measure of the line of sight component of displacement only. This can be converted to a vertical displacement using trigonometry but this assumes that all of the motion was actually vertical. Earthquakes for example can produce displacements in any direction. Second, it can be difficult to tell if a positive value refers to uplift or subsidence. Because the previous recipes in this series used the earlier SLC as the master image, we are assuming the positive value refers to uplift. In the phase values, the opposite is true since this is a measure of how much the satellite has moved away from the ground, not the other way around. The phase to displacement conversion includes a negative sign which corrects for this.

Background

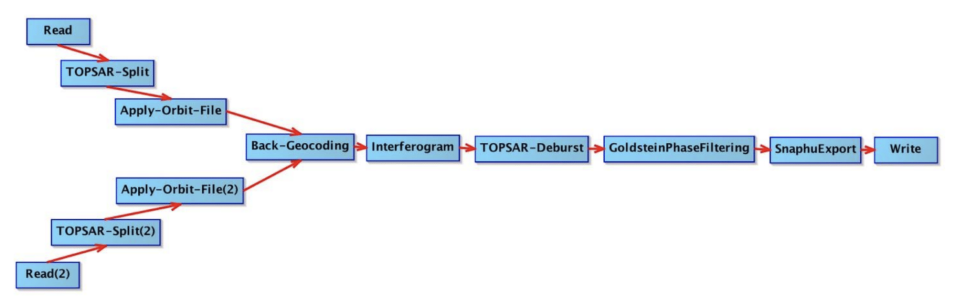
This recipe covers the final steps in deriving displacement data from a Sentinel-1 SLC pair (and interferogram), and builds on two other ASF Data Recipes. A wrapped interferogram is generated using the ASF Create an Interferogram data recipe, then the ASF Phase Unwrapping recipe walks you through unwrapping the interferogram. This recipe picks up where the Phase Unwrapping recipe left off.

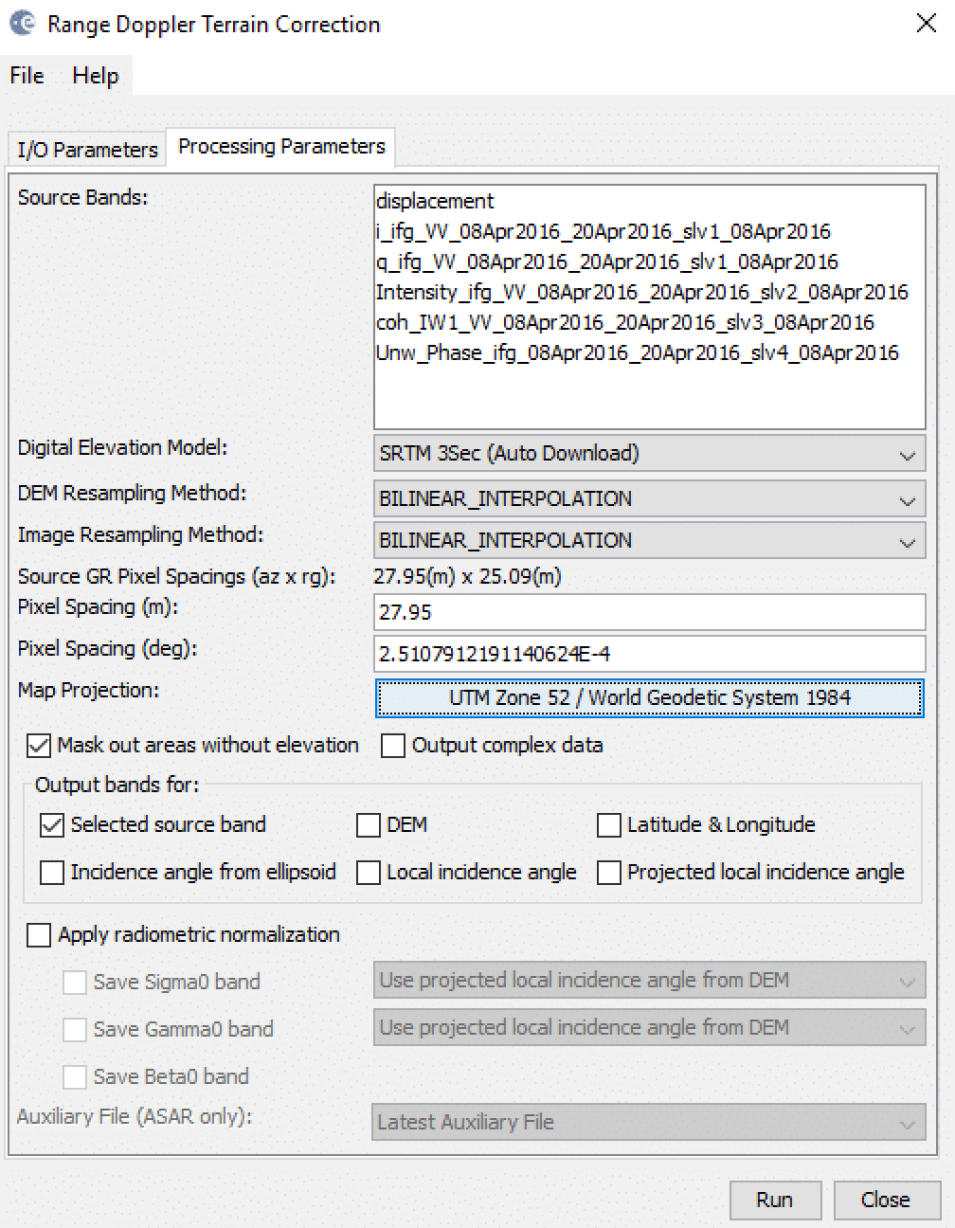
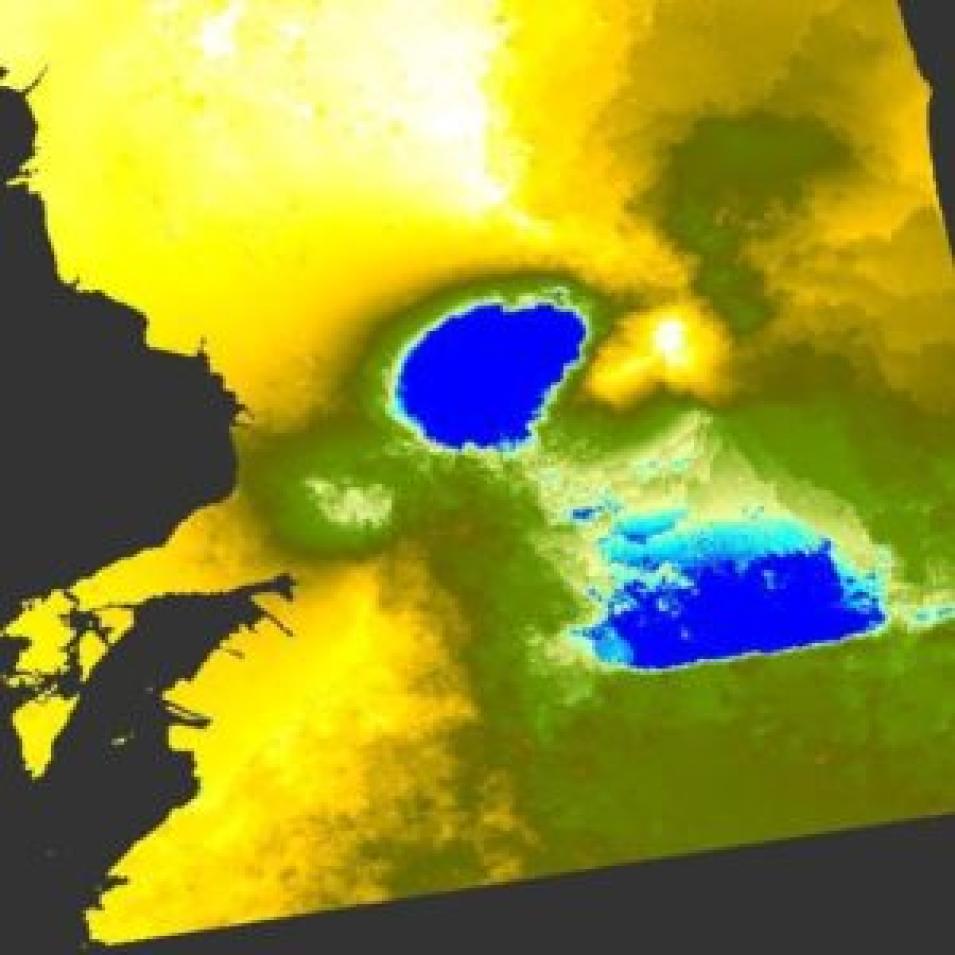
In order to create a deformation map from an unwrapped interferogram, phase values must first be converted to displacement (in meters). This displacement value is derived from the differential phase values in the line of sight of Sentinel-1. Hence, the displacement value will also be relative to the sensor at the look angle, or angle of incidence, and not an absolute vertical displacement.

Coherence values must also be determined in order to assess the validity of our displacement map. In general, coherence measures how well the two images that formed the interferogram are correlated. In the context of SAR remote sensing, this assessment is estimated from the random noise and amplitude differences that exist within a resolution cello, or pixel as viewed in the S1TBX. Areas of decorrelation (loss of coherence) should be ignored when interpreting accurate displacement values.

Coherence loss is cumulative from multiple sources:

Temporal changes such as the growth/movement/harvest of vegetation or snow accumulation/melting between the two SLC images
A low signal-to-noise ratio
Weak signal return
Altitude changes in the range or azimuth direction (coherence loss is most severe when this difference is within a resolution cell)

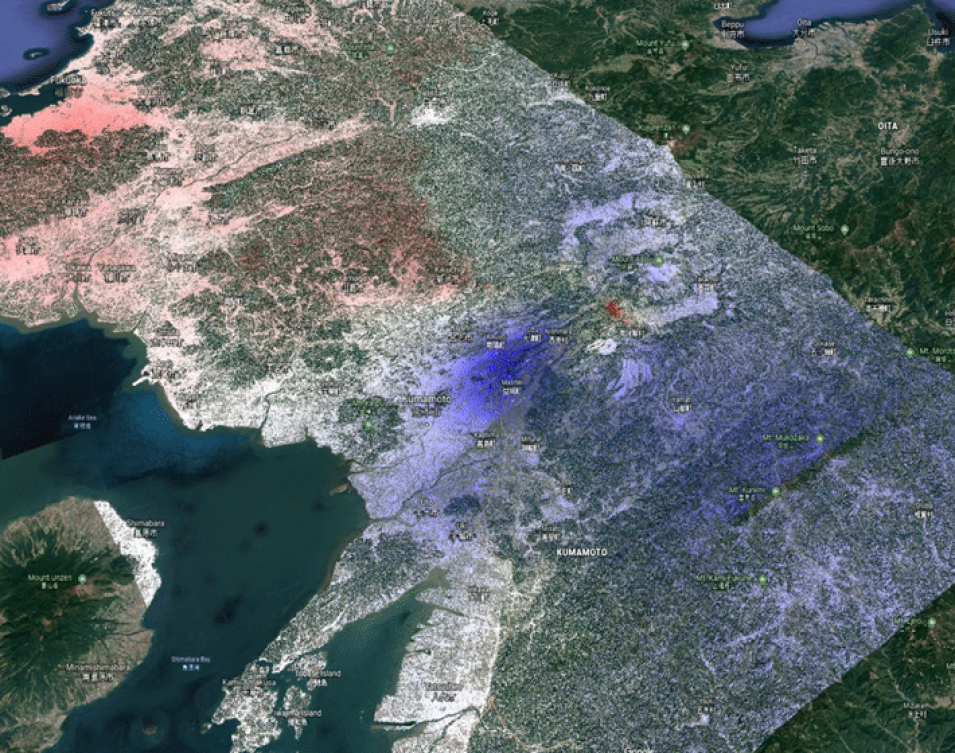
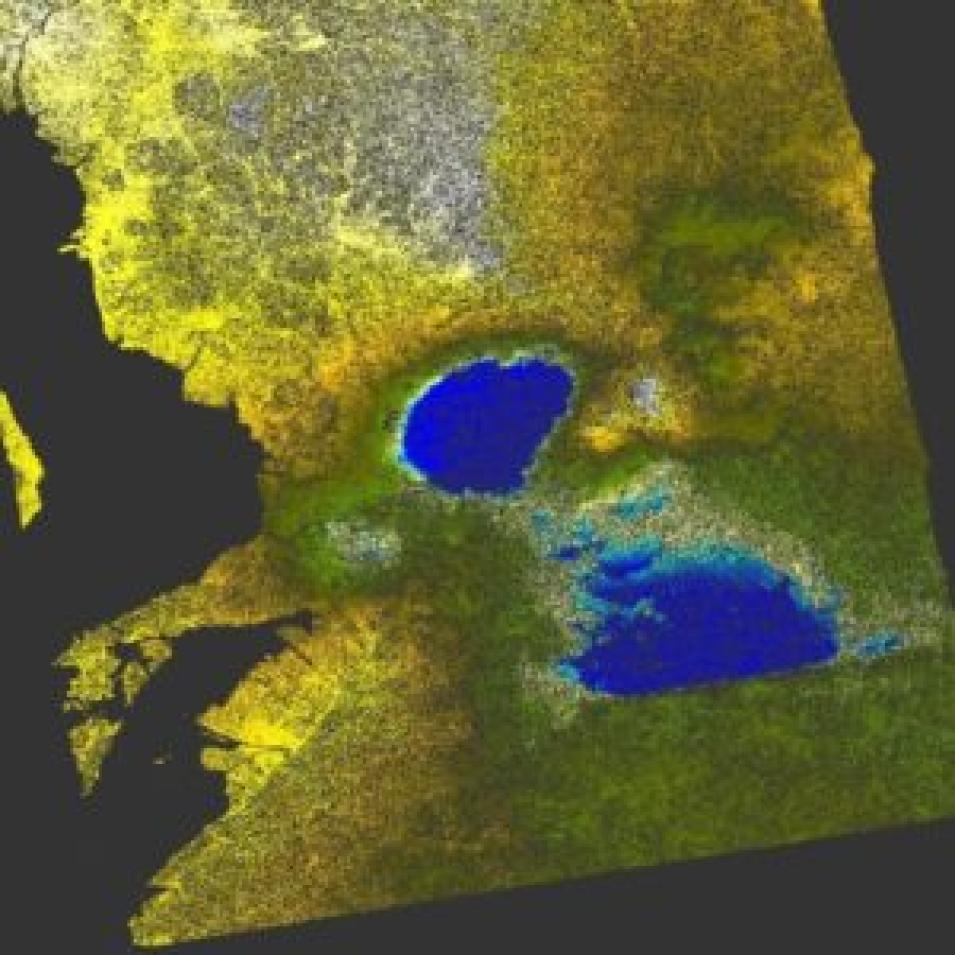
Consequently, coherence tends to be highest in urban areas due to low temporal decorrelation and high backscatter intensities. Low coherence is indicative of water bodies and areas with a high vegetation index. Processes such as erosion and deposition can also cause decorrelation depending on the degree of backscatter divergence.

This is exemplified in the area surrounding the cities Kumamoto and Fukuoka in Japan (Figure 1). In this image indicating coherence levels, the Chikugo River (top left) is easily visible as a result of its low coherence (dark) values in contrast to the surrounding bright urban areas. Compared with an optical view from Google Earth (Figure 2), highly vegetated and undeveloped areas correlate with lower coherence.

Figure 1: Geocoded coherence band. Contains modified Copernicus Sentinel data (2016) processed by ESA.

Figure 2: Kumamoto and Fukuoka cities viewed in Google Earth. Imagery © 2018 Landsat/Copernicus, Data SIO, NOAA, U.S. Navy, NGA, GEBCO. Map Data © 2018 Google, SK telecom, ZENRIN.

Prerequisites

System Requirements

Windows, Mac OS X, or Unix computing environment
16 GB RAM
At least 50 GB of available disk space

Note: A Solid State Drive will perform significantly faster than a Hard Disk Drive and when processing large files, this will be very advantageous. If you encounter an error in the middle of a processing step, it may be because your disk is full.

Materials List

The latest version of Sentinel-1 Toolbox (S1TBX).
- The software that runs S1TBX is called SNAP. Open the application by double-clicking the desktop icon, or searching for SNAP software among your computer programs. The software can be downloaded from the ESA SNAP Download page.
- Make sure that any available updates have been applied. A message will usually display in the bottom right corner when updates are available, but you can also check by selecting Check for Updates from the Help menu.
The unwrapped interferogram with phase and coherence bands (Figure 4) generated by following the ASF Phase Unwrapping data recipe.
- If the product is not already open in S1TBX, open the .dim file of the unwrapped phase (not Geocoded/Terrain Corrected).
- The following source granules are used to generate the interferogram that is subsequently unwrapped and used in this recipe. They are provided for reference only, but if you have not yet followed the previous two recipes, you will need to download them.

Pre-event sample SLC:
S1A_IW_SLC_1SSV_20160408T091355_20160408T091430_010728_01001F_83EB
Post-event sample SLC:
S1A_IW_SLC_1SSV_20160420T091355_20160420T091423_010903_010569_F9CE

Pre-Processing Review

Create a Differential Interferogram

Detailed information on completing this procedure is covered in the ASF Interferogram Generation data recipe. The diagram shown in Figure 3 and the list of the processing steps, which reference the menu options leading to the tool for each step, give an overview of the steps required to generate a wrapped interferogram.

Pre-unwrapping Interferogram Formation steps (without geocoding/terrain correction).

Figure 3: Visualization of the interferogram generation workflow.

a) Coregistration
Radar > Coregistration > S1 TOPS Coregistration > S-1 TOPS Coregistration

b) Create Interferogram
Radar > Interferometric > Products > Interferogram Formation

c) Deburst
Radar > Sentinel-1 TOPS > S-1 Deburst

d) Topographic Phase Removal
Radar > Interferometric > Products > Topographic Phase Removal

e) Multilook
Radar > Multilooking

f) Goldstein Phase Filtering
Radar > Interferometric > Filtering > Goldstein Phase Filtering

Note: This process chain does not include a Geocoding step. This will be done near the end of this recipe, once the deformation map is generated.

If you geocoded the Unwrapped Interferogram in the previous recipe, make sure to use the product from the step prior to geocoding (not tagged with a _TC) for the next step.

Unwrap the Interferogram

Detailed information on completing this procedure is covered in the ASF Phase Unwrapping data recipe. A brief overview of the steps in that process is presented below.

a) Snaphu Export
Radar > Interferometric > Unwrapping > Snaphu Export

b) Snaphu Unwrapping in a Linux command line

c) Snaphu Import
Radar > Interferometric > Unwrapping > Snaphu Import

Note: This process chain again does not include a Geocoding step. This will be done near the end of this recipe, once the deformation map is generated.

If you Geocoded the Unwrapped Interferogram in the previous recipe, make sure to use the product from the step prior to geocoding (not tagged with a _TC) for this next step.

At this point, you should have an unwrapped interferogram (Figure 4) loaded into the Sentinel-1 Toolbox (S1TBX). This recipe will resume from here.

Figure 4: Segment of a snaphu imported unwrapped interferogram (without Terrain Correction). Contains modified Copernicus Sentinel data (2016) processed by ESA.

Steps to Create a Deformation Map

Step 1: Convert Phase to Displacement

This step converts the unwrapped differential phase value (radians) to a displacement value (in meters) along the line of sight of the sensor.

This is computed using the following equation:

Where λ is Sentinel-1’s C-band SAR wavelength and is the unwrapped phase difference between the two SLC images.

1. Select the imported and unwrapped interferogram in the Product Explorer window in S1TBX. If the Product Explorer window is not open, select Tool Windows from the View menu and select Product Explorer to open it.

2. Navigate to Radar > Interferometric > Products > Phase to Displacement.

3. In the Phase to Displacement window, specify the output folder and the target product name.

The products will automatically be appended with the suffix “_dsp” if you choose the default name.
There will be no options available in the Processing Parameters tab. Click <Run> and allow the image to be processed. The new product, appearing in the Product Explorer window, will have a single band (Figure 5).

Figure 5: Segment of the resultant displacement map. Contains modified Copernicus Sentinel data (2016) processed by ESA.

Estimating Vertical Displacement Using Band Maths

Vertical displacement can be estimated if it’s assumed that there is no horizontal motion parallel to the sensor’s line of sight. This can be computed via Band Maths instead of the Phase to Displacement operator.

These steps using Band Maths are included as extra information only; the rest of this recipe uses the line-of-sight displacement band generated with the Phase to Displacement operator in the previous step.

Absolute vertical displacement in a setting with no horizontal movement can be calculated with the following expression, where the number 0.056 is the approximate value of Sentinel-1’s wavelength in meters:

(0.056 * Unw_Phase_ifg_08Apr2016_20Apr2016) / (-4 * PI * cos(rad(incident_angle)))

1. In the Product Explorer, right click the unwrapped interferogram product and select Band Maths.

2. In the Band Maths window (Figure 8), set the Name to something appropriate, such as Vertical_Displacement.

a. Enter meters in the Unit field.
b. Uncheck Virtual.
c. In the Band maths expression field, paste the expression listed above.

3. Click <OK>. The new band will appear in the bands directory and when viewed, should look very similar to Figure 5.

Step 2: Create Stack

The Phase to Displacement operation outputs only one band. To verify the accuracy of our data, we still need the coherence band created when the interferogram was first generated. Creating a stack will merge the _dsp product with the imported unwrapped interferogram.

1. Navigate to Radar > Coregistration > Stack Tools > Create Stack.

2. In the ProductSet-Reader tab of the Create Stack window, select the unwrapped interferogram and the _dsp product created in Step 1.

3. In the Write tab, specify the target product name and the output folder. The products will automatically be appended with the suffix “_Stack” if you choose the default name.

4. Click <Run> and allow the stack to be formed. The new product will appear in the Product Explorer window and will include the bands from both products.

Step 3: Range-Doppler Terrain Correction

The Range-Doppler Terrain Correction operator applies a series of processes to the displacement map.

First, it uses a Digital Elevation Model (DEM) to mask out areas without any elevation, including the ocean. This is helpful because none of the phase or displacement data over the ocean is useful.

Second, it uses the DEM and a map projection system to orthorectify the image, projecting it onto the Earth’s surface in its proper orientation. This operator also geometrically corrects SAR data, but this is not as relevant to this procedure as we only care about the included displacement and coherence bands which no longer include terrain geometry.

1. Select your _Stack product in the Product Explorer

2. From the menu bar, navigate to Radar > Geometric > Terrain Correction > Range-Doppler Terrain Correction.

3. In the I/O Parameters tab in the Range-Doppler Terrain Correction window, specify the target product name and the output folder. The products will automatically be appended with the suffix “_TC” if you choose the default name.

4. In the Processing Parameters tab (Figure 6), set the Map Projection by clicking on the Map Projection option. In the window that appears, select UTM Zone / WGS 84 (Automatic) from the Projection options. This will apply the appropriate UTM zone for the image location (best for GIS).

NOTE: If you want to export KMZ files for use in Google Earth as your primary product, leave the Map Projection as WGS84(DD).

Also note that the SRTM, which is the default DEM, does not have coverage beyond 60 degrees north and south. If your granules are located above 60 degrees north, you will need to select a DEM that covers that area, such as ACE30.

5. Leave the rest of the parameters as default and click <Run>.

6. When processing is complete, close the Correction window and view the product (Figure 7) by double-clicking the band.

Figure 6: Range Doppler Terrain Correction Processing Parameters.

Figure 7: Geocoded displacement map. Contains modified Copernicus Sentinel data (2016) processed by ESA.

Step 4: Mask Out Areas of Low Coherence

1. In the Product Explorer, right-click the terrain corrected displacement map stack created in Step 3 and select Band Maths.

Figure 8: Band Maths Window.

2. In the Band Maths window (Figure 8), set the Name to something appropriate, such as Masked Displacement.

3. Copy and paste the following expression into the Band maths expression field:

if coh_IW1_VV_20Apr2016_08Apr2016 > .3 then displacement_slv1_20Apr2016_VV else NaN

4. Click <OK>. A new band will appear in the product’s Bands folder, and the image will appear in the view area (Figure 9).

Figure 9: Displacement map with areas of low coherence masked out. Contains modified Copernicus Sentinel data (2016) processed by ESA

This Band Maths expression will create a new displacement band where areas of low coherence (unreliable data) are removed. If the coherence value is greater than 0.3 (on a scale from 0 to 1), the new band will use values from the displacement band. If the coherence value is 0.3 or less, the pixel will be set to a NoData value.

The threshold can be set to any value, and you may find that you require a different value depending on the situation. You can easily build your own expression by clicking the Edit Expression button.

Step 5: Update Color Scheme

1. Ensure that the masked displacement band is open and displayed in the view area.

2. Click on the Colour Manipulation tab in the lower left corner of S1TBX to view the Color Manipulation window (Figure 10). If the Colour Manipulation window is not open, select Tool Windows from the View menu and select Colour Manipulation to open it.

3. Click the circle by Sliders in the top left corner of the window if necessary to open the Sliders Editor view (see Figure 10).

4. Click on the Rough Statistics! text in the top right of the graph pane and click <Yes> in order to calculate accurate displacement statistics for the color scheme.

5. Select the Basic view in the top left region of the tab. Select great_circle from the colour ramp options, and click the Range from Data button.

6. Return to the Sliders view. Right-click the triangle slider on the far left of the color scale and select Remove Slider.

There are two sliders almost on top of each other on the left side of the color ramp, and this will remove the extra one.

7. Select the Table view. There should be three entries with data values listed for each color: blue, white and red. If the first color is black, click on the colour patch and change it to blue. Double-click on the value next to white and change it to 0. Press Enter to apply the change. If there are more than three values, return to the Sliders view and remove the extra sliders.

The resulting displacement map (Figure 11) displays the change in the distance along the line-of-sight from the sensor to the earth’s surface.

If the image acquired on the earlier date was used as the master in this process, positive values (displayed in red on this color scale) will indicate areas that are closer to the sensor in the later acquisition than they were in the earlier acquisition. This could indicate either vertical uplift or horizontal displacement in the direction towards the sensor, but is most often a combination of both.

Figure 11: Displacement map colored with red indicating uplift, blue subsidence, and white no change.

Negative values (displayed in blue on this color scale) indicate either subsidence or horizontal displacement in the direction away from the sensor, but again is most often a combination of both. Areas displayed in white indicate regions without change.

Step 6: Export as GeoTIFF

1. Right-click in the view area on your masked and re-colored displacement map. Select Export View as Image, and save the file.

2. In the upper right-hand side of the new window (Figure 12), select Full Screen.

3. Next to Files of type select GeoTIFF.

Figure 12: Export View as Image window

4. Click <Save>.

View in Google Earth (OPTIONAL)

To export to KMZ format, the Masked Displacement band must be in a Geographic Coordinate System (lat/lon). If you output to a UTM projection during Terrain Correction in Step 3, you will need to reproject the output to WGS 84 (Figure 13). Alternatively, you can rerun Step 3 projecting to WGS 84 instead of UTM, then repeat Steps 4 and 5.

Subset Bands (OPTIONAL)

It takes a while to reproject an entire stack, so you may wish to create a subset with only the bands required for the Masked Displacement output first before reprojecting.

1. Select the final product (which includes the Masked Displacement band), and from the menu bar, navigate to Raster > Subset.

2. Select the Band Subset tab and select only the Masked Displacement, coh and displacement bands. Note that if you only select the Masked Displacement band, S1TBX pops up a window prompting you to select the reference datasets (coherence and displacement) as well.

3. Click <OK> to generate the subset. The output will be prefixed with subset and added to the Product Explorer.

Reproject Subset Bands

Select the subset product (or the full product including the Masked Displacement if you want to reproject all of the bands) in the Product Explorer.

1. From the menu bar, navigate to Raster > Geometric Operations > Reprojection.

2. Make sure that the source in the I/O Parameters tab is your final product, including the Masked Displacement band, and tag the output file as desired (you may wish to add an indication that it is projected to WGS84).

3. In the Reprojection Parameters tab, change the Projection to Geographic Lat/Lon (WGS 84) if necessary, and change the Resampling method to Bilinear.

4. Click <Run> to generate the reprojected output.

5. You will need to reset the color scheme of the Masked Displacement band in the output raster (see Step 5); it will revert to the default color settings in the reprojection process.

Export Masked Displacement Band to KMZ

Double-click on the final Masked Displacement band (projected to WGS84) in the Product Explorer to view the band. Zoom or pan to the desired extent for the KMZ export.

1. Right-click in the view area on your masked and re-colored displacement map. Select Export View as Google Earth KMZ, and save the file.

2. Open Google Earth in your web browser. Wait for the web application to load.

3. Click the Bookmark Icon in the toolbar along the left side of the screen. Hovering over it will reveal the label My Places.

4. Click Import KML File > Open File and select your exported displacement map. Google Earth will overlay the map and zoom to the geographic area (Figure 14).

Considerations

Uplift or Subsidence?

The sign on our displacement maps can at sometimes be ambiguous. Interpreting the direction of displacement must be done carefully with respect to the master and slave combination of your two SLCs, as well as the expression used when converting the unwrapped phase interferogram to displacement. Recall that the Sentinel-1 Toolbox uses the following formula where λ is Sentinel-1’s C-Band SAR wavelength and ΔΦd is the unwrapped phase difference between the two SLCs.

Notice how this also includes a negative sign, implying that our displacement values will be opposite those of the unwrapped interferogram. This makes sense if you think about what the phase values actually mean. Our interferogram was created in the frame of reference of the satellite, meaning that the unwrapped phase values correspond to how much the distance between the surface and the satellite has changed. An increasing phase value indicates that this distance is increasing and what this actually corresponds to on the ground is subsidence. In this way, a positive unwrapped phase value will correspond with a negative displacement on the ground.

The alternative way to reach this same result is by choosing the second image in the pair as master. In this case, the phase values would be with respect to the post-event image and the sign of the phase values will correspond to the sign of the displacement. Instead of using the Sentinel-1 Toolbox’s default expression, you would have to use band maths to manually generate the displacement map, remembering to exclude the negative sign from the expression.

If you’re attempting to interpret a deformation map where you are unsure of the expression used to calculate the displacement, the best way to verify the sign on your displacement values is to compare a point to known ground truth data. If your area of study is known to follow a certain behavior such as subsidence as a result of aquifer depletion then this can also be used. Deforming volcanos and earthquake fault ruptures will produce less predictable results, however, so it’s best to use caution in these situations and consult ground truth data if it’s available.

Sentinel-1 Toolbox and SNAPHU Limitations

If you were to compare the deformation map generated in this tutorial to products generated using the same base granules with other software, you will notice some differences. The most obvious changes will manifest during the unwrapping stage. This is primarily because of the lower coherence of the Sentinel-1 Toolbox interferogram. During the unwrapping stage, decorrelated regions may cause unwrapping errors and regions of subsidence may bleed into regions where uplift actually occurred. Unfortunately, this is the case for the deformation map created in this recipe. Other software packages with more accurate co-registration processors may increase coherence.

Atmospheric Error

Interferograms can be impacted by differences in atmospheric conditions, particularly the presence of water vapor, at the time of the two acquisitions. The impacts of atmospheric error can be mitigated by using software that implements atmospheric models to correct for this difference. InSAR Time Series analysis can also be used to help reduce the impact of atmospheric error. It is important to note that atmospheric errors are still present after low coherence areas have been masked out, as atmospheric conditions only impact the phase and distance measurements without impacting coherence.

Dataset Information

Dataset Name	Format
Sentinel-1

Details

Last Updated

Feb 3, 2025

Published on

Feb 3, 2025

Author

ASF Staff

Data Centers

Alaska Satellite Facility DAAC (ASF DAAC)